二分查找法模板的基本思想-leetcode35

leetcode35

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

示例 1:

输入: [1,3,5,6], 5
输出: 2
示例 2:

输入: [1,3,5,6], 2
输出: 1
示例 3:

输入: [1,3,5,6], 7
输出: 4
示例 4:

输入: [1,3,5,6], 0
输出: 0

传统解法：

public class Solution3 {

    public int searchInsert(int[] nums, int target) {
        int len = nums.length;
        if (nums[len - 1] < target) {
            return len;
        }

        int left = 0;
        int right = len - 1;

        while (left <= right) {
            int mid = (left + right) / 2;
            // 等于的情况最简单，我们应该放在第 1 个分支进行判断
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                // 题目要我们返回大于或者等于目标值的第 1 个数的索引
                // 此时 mid 一定不是所求的左边界，
                // 此时左边界更新为 mid + 1
                left = mid + 1;
            } else {
                // 既然不会等于，此时 nums[mid] > target
                // mid 也一定不是所求的右边界
                // 此时右边界更新为 mid - 1
                right = mid - 1;
            }
        }
        // 注意：一定得返回左边界 left，
        // 如果返回右边界 right 提交代码不会通过
        // 【注意】下面我尝试说明一下理由，如果你不太理解下面我说的，那是我表达的问题
        // 但我建议你不要纠结这个问题，因为我将要介绍的二分查找法模板，可以避免对返回 left 和 right 的讨论

        // 理由是对于 [1,3,5,6]，target = 2，返回大于等于 target 的第 1 个数的索引，此时应该返回 1
        // 在上面的 while (left <= right) 退出循环以后，right < left，right = 0 ，left = 1
        // 根据题意应该返回 left，
        // 如果题目要求你返回小于等于 target 的所有数里最大的那个索引值，应该返回 right

        return left;
    }
}

说明

a、当把二分查找法的循环可以进行的条件写成 while (left <= right) 时，在写最后一句 return 的时候，如果不假思索，把左边界 left 返回回去，虽然写对了，但可以思考一下为什么不返回右边界 right 呢？

b、但是事实上，返回 left 是有一定道理的，如果题目换一种问法，你可能就要返回右边界 right，这句话不太理解没有关系，我也不打算讲得很清楚（在上面代码的注释中我已经解释了原因），因为实在太绕了，这不是我要说的重点。

二分查找法模板的基本思想

1、首先把循环可以进行的条件写成 while(left < right)，在退出循环的时候，一定有 left == right 成立，此时返回 left 或者 right 都可以
或许你会问：退出循环的时候还有一个数没有看啊（退出循环之前索引 left 或 索引 right 上的值）？
没有关系，我们就等到退出循环以后来看，甚至经过分析，有时都不用看，就能确定它是目标数值。

（什么时候需要看最后剩下的那个数，什么时候不需要，会在后面介绍。）

更深层次的思想是“夹逼法”或者称为“排除法”。

2、“神奇的”二分查找法模板的基本思想（特别重要）
“排除法”即：在每一轮循环中排除一半以上的元素，于是在对数级别的时间复杂度内，就可以把区间“夹逼” 只剩下 1 个数，而这个数是不是我们要找的数，单独做一次判断就可以了。

“夹逼法”或者“排除法”是二分查找算法的基本思想，“二分”是手段，在目标元素不确定的情况下，“二分” 也是“最大熵原理”告诉我们的选择。

还是 LeetCode 第 35 题，下面给出使用 while (left < right) 模板写法的 2 段参考代码，以下代码的细节部分在后文中会讲到，因此一些地方不太明白没有关系，暂时跳过即可。

参考代码 1：重点理解为什么候选区间的索引范围是 [0, size]。

from typing import List

class Solution:

    def searchInsert(self, nums: List[int], target: int) -> int:
        # 返回大于等于 target 的索引，有可能是最后一个
        size = len(nums)
        # 特判
        if size == 0:
            return 0

        left = 0
        # 如果 target 比 nums里所有的数都大，则最后一个数的索引 + 1 就是候选值，因此，右边界应该是数组的长度
        right = size
        # 二分的逻辑一定要写对，否则会出现死循环或者数组下标越界
        while left < right:
            mid = left + (right - left) // 2
            if nums[mid] < target:
                left = mid + 1
            else:
                assert nums[mid] >= target
                # [1,5,7] 2
                right = mid
        # 调试语句
        # print('left = {}, right = {}, mid = {}'.format(left, right, mid))
        return left

      

参考代码 2：对于是否接在原有序数组后面单独判断，不满足的时候，再在候选区间的索引范围 [0, size - 1] 内使用二分查找法进行搜索。

from typing import List


class Solution:

    def searchInsert(self, nums: List[int], target: int) -> int:
        # 返回大于等于 target 的索引，有可能是最后一个
        size = len(nums)
        # 特判 1
        if size == 0:
            return 0
        # 特判 2：如果比最后一个数字还要大，直接接在它后面就可以了
        if target > nums[-1]:
            return size

        left = 0
        right = size - 1
        # 二分的逻辑一定要写对，否则会出现死循环或者数组下标越界
        while left < right:
            mid = left + (right - left) // 2
            if nums[mid] < target:
                left = mid + 1
            else:
                assert nums[mid] >= target
                right = mid
        return left

细节、注意事项、调试方法

1、前提：思考左、右边界，如果左、右边界不包括目标数值，会导致错误结果
例：LeetCode 第 69 题：x 的平方根

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

分析：一个非负整数的平方根最小可能是 0 ，最大可能是它自己。
因此左边界可以取 0 ，右边界可以取 x。
可以分析得再细一点，但这道题没有必要，因为二分查找法会帮你排除掉不符合的区间元素。

例：LeetCode 第 287 题：寻找重复数

给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。

分析：题目告诉我们“其数字都在 1 到 n 之间（包括 1 和 n）”。因此左边界可以取 1 ，右边界可以取 n。

要注意 2 点：

如果 left 和 right 表示的是数组的索引，就要考虑“索引是否有效” ，即“索引是否越界” 是重要的定界依据；

左右边界一定要包括目标元素，例如 LeetCode 第 35 题：“搜索插入位置” ，当 target 比数组中的最后一个数字还要大（不能等于）的时候，插入元素的位置就是数组的最后一个位置 + 1，即 (len - 1 + 1 =) len，如果忽略掉这一点，把右边界定为 len - 1 ，代码就不能通过在线测评。

2、中位数先写 int mid = (left + right) >>> 1 ; 根据循环里分支的编写情况，再做调整
理解这一点，首先要知道：当数组的元素个数是偶数的时候，中位数有左中位数和右中位数之分。

当数组的元素个数是偶数的时候：
使用 int mid = left + (right - left) / 2 ; 得到左中位数的索引；

使用 int mid = left + (right - left + 1) / 2 ; 得到右中位数的索引。

当数组的元素个数是奇数的时候，以上二者都能选到最中间的那个中位数。
其次，

int mid = left + (right - left) / 2 ; 等价于 int mid = (left + right) >>> 1；

int mid = left + (right - left + 1) / 2 ; 等价于 int mid = (left + right + 1) >>> 1 。

我们使用一个具体的例子来验证：当左边界索引 left = 3，右边界索引 right = 4 的时候，

mid1 = left + (right - left) // 2 = 3 + (4 - 3) // 2 = 3 + 0 = 3，

mid2 = left + (right - left + 1) // 2 = 3 + (4 - 3 + 1) // 2 = 3 + 1 = 4。

左中位数 mid1 是索引 left，右中位数 mid2 是索引 right。

记忆方法：

(right - left) 不加 11 选左中位数，加 11 选右中位数。

那么，什么时候使用左中位数，什么时候使用右中位数呢？选中位数的依据是为了避免死循环，得根据分支的逻辑来选择中位数，而分支逻辑的编写也有技巧，下面具体说。

3、先写逻辑上容易想到的分支逻辑，这个分支逻辑通常是排除中位数的逻辑；
在逻辑上，“可能是也有可能不是”让我们感到犹豫不定，但**“一定不是”是我们非常坚决的，通常考虑的因素特别单一，因此“好想” **。在生活中，我们经常听到这样的话：找对象时，“有车、有房，可以考虑，但没有一定不要”；找工作时，“事儿少、离家近可以考虑，但是钱少一定不去”，就是这种思想的体现。

例：LeetCode 第 69 题：x 的平方根

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

分析：因为题目中说“返回类型是整数，结果只保留整数的部分，小数部分将被舍去”。例如 55 的平方根约等于 2.2362.236，在这道题应该返回 22。因此如果一个数的平方小于或者等于 x，那么这个数有可能是也有可能不是 x 的平方根，但是能很肯定的是，如果一个数的平方大于 x ，这个数肯定不是 x 的平方根。

注意：先写“好想”的分支，排除了中位数之后，通常另一个分支就不排除中位数，而不必具体考虑另一个分支的逻辑的具体意义，且代码几乎是固定的。

4、循环内只写两个分支，一个分支排除中位数，另一个分支不排除中位数，循环中不单独对中位数作判断
既然是“夹逼”法，没有必要在每一轮循环开始前单独判断当前中位数是否是目标元素，因此分支数少了一支，代码执行效率更高。

以下是“排除中位数的逻辑”思考清楚以后，可能出现的两个模板代码。

可以排除“中位数”的逻辑，通常比较好想，但并不绝对，这一点视情况而定。

分支条数变成 2 条，比原来 3 个分支要考虑的情况少，好处是：

不用在每次循环开始单独考虑中位数是否是目标元素，节约了时间，我们只要在退出循环的时候，即左右区间压缩成一个数（索引）的时候，去判断这个索引表示的数是否是目标元素，而不必在二分的逻辑中单独做判断。

这一点很重要，希望读者结合具体练习仔细体会，每次循环开始的时候都单独做一次判断，在统计意义上看，二分时候的中位数恰好是目标元素的概率并不高，并且即使要这么做，也不是普适性的，不能解决绝大部分的问题。

还以 LeetCode 第 35 题为例，通过之前的分析，我们需要找到“大于或者等于目标值的第 1 个数的索引”。对于这道题而言：

• 如果中位数小于目标值，它就应该被排除，左边界 left 就至少是 mid + 1；

• 如果中位数大于等于目标值，还不能够肯定它就是我们要找的数，因为要找的是等于目标值的第 11 个数的索引，中位数以及中位数的左边都有可能是符合题意的数，因此右边界就不能把 mid 排除，因此右边界 right 至多是 mid，此时右边界不向左边收缩。

下一点就更关键了。

5、根据分支逻辑选择中位数的类型，可能是左中位数，也可能是右位数，选择的标准是避免死循环

死循环容易发生在区间只有 22 个元素时候，此时中位数的选择尤为关键。选择中位数的依据是：避免出现死循环。我们需要确保：

（下面的这两条规则说起来很绕，可以暂时跳过）。

• 如果分支的逻辑，在选择左边界的时候，不能排除中位数，那么中位数就选“右中位数”，只有这样区间才会收缩，否则进入死循环；

• 同理，如果分支的逻辑，在选择右边界的时候，不能排除中位数，那么中位数就选“左中位数”，只有这样区间才会收缩，否则进入死循环。

理解上面的这个规则可以通过具体的例子。针对以上规则的第 1 点：如果分支的逻辑，在选择左边界的时候不能排除中位数，例如：

while left < right:
      # 不妨先写左中位数，看看你的分支会不会让你代码出现死循环，从而调整
    mid = left + (right - left) // 2
    # 业务逻辑代码
    if (check(mid)):
        # 选择右边界的时候，可以排除中位数
        right = mid - 1
    else:
        # 选择左边界的时候，不能排除中位数
        left = mid

在区间中的元素只剩下 22 个时候，例如：left = 3，right = 4。此时左中位数就是左边界，如果你的逻辑执行到 left = mid 这个分支，且你选择的中位数是左中位数，此时左边界就不会得到更新，区间就不会再收缩（理解这句话是关键），从而进入死循环；
为了避免出现死循环，你需要选择中位数是右中位数，当逻辑执行到 left = mid 这个分支的时候，因为你选择了右中位数，让逻辑可以转而执行到 right = mid - 1 让区间收缩，最终成为 1 个数，退出 while 循环。
上面这段话不理解没有关系，因为我还没有举例子，你有个印象就好，类似地，理解选择中位数的依据的第 2 点。

6、退出循环的时候，可能需要对“夹逼”剩下的那个数单独做一次判断，这一步称之为“后处理”。
二分查找法之所以高效，是因为它利用了数组有序的特点，在每一次的搜索过程中，都可以排除将近一半的数，使得搜索区间越来越小，直到区间成为一个数。回到这一节最开始的疑问：“区间左右边界相等（即收缩成 1 个数）时，这个数是否会漏掉”，解释如下：

• 如果你的业务逻辑保证了你要找的数一定在左边界和右边界所表示的区间里出现，那么可以放心地返回 left 或者 right，无需再做判断；

• 如果你的业务逻辑不能保证你要找的数一定在左边界和右边界所表示的区间里出现，那么只要在退出循环以后，再针对 nums[left] 或者 nums[right] （此时 nums[left] == nums[right]）单独作一次判断，看它是不是你要找的数即可，这一步操作常常叫做“后处理”。

如果你能确定候选区间里目标元素一定存在，则不必做“后处理”。
例：LeetCode 第 69 题：x 的平方根

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

分析：非负实数 x 的平方根在 [0, x] 内一定存在，故退出 while (left < right) 循环以后，不必单独判断 left 或者 right 是否符合题意。

如果你不能确定候选区间里目标元素一定存在，需要单独做一次判断。
例：LeetCode 第 704 题：二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

分析：因为目标数有可能不在数组中，当候选区间夹逼成一个数的时候，要单独判断一下这个数是不是目标数，如果不是，返回 -1。

7、取中位数的时候，要避免在计算上出现整型溢出；
int mid = (left + right) / 2; 的问题：在 left 和 right 很大的时候，left + right 会发生整型溢出，变成负数，这是一个 bug ，得改！

int mid = left + (right - left) / 2; 在 right 很大、 left 是负数且很小的时候， right - left 也有可能超过 int 类型能表示的最大值，只不过一般情况下 left 和 right 表示的是数组索引值，left 是非负数，因此 right - left 溢出的可能性很小。因此，它是正确的写法。下面介绍推荐的写法。

int mid = (left + right) >>> 1; 如果这样写， left + right 在发生整型溢出以后，会变成负数，此时如果除以 22 ，mid 是一个负数，但是经过无符号右移，可以得到在不溢出的情况下正确的结果。

解释“无符号右移”：在 Java 中，无符号右移运算符 >>> 和右移运算符 >> 的区别如下：

右移运算符 >> 在右移时，丢弃右边指定位数，左边补上符号位；
无符号右移运算符 >>> 在右移时，丢弃右边指定位数，左边补上 00，也就是说，对于正数来说，二者一样，而负数通过 >>> 后能变成正数。
下面解释上面的模板中，取中位数的时候使用先用“＋”，然后“无符号右移”。

a、int mid = (left + right) / 2 与 int mid = left + (right - left) / 2 两种写法都有整型溢出的风险，没有哪一个是绝对安全的，注意：这里我们取平均值用的是除以 2，并且是整除：

int mid = (left + right) / 2 在 left 和 right 都很大的时候会溢出；
int mid = left + (right - left) / 2 在 right 很大，且 left 是负数且很小的时候会溢出；
b、写算法题的话，一般是让你在数组中做二分查找，因此 left 和 right 一般都表示数组的索引，因此 left 在绝大多数情况下不会是负数并且很小，因此使用 int mid = left + (right - left) // 2 相对 int mid = (left + right) // 2 更安全一些，并且也能向别人展示我们注意到了整型溢出这种情况，但事实上，还有更好的方式；

c、建议使用 int mid = (left + right) >>> 1 这种写法，其实是大有含义的：

JDK8 中采用 int mid = (left + right) >>> 1 ，重点不在 + ，而在 >>> 。

我们看极端的情况，left 和 high 都是整型最大值的时候，注意，此时 3232 位整型最大值它的二进制表示的最高位是 00，它们相加以后，最高位是 11 ，变成负数，但是再经过无符号右移 >>>（重点是忽略了符号位，空位都以 00 补齐），就能保证使用 + 在整型溢出了以后结果还是正确的。

Java 中 Collections 和 Arrays 提供的 binarySearch 方法，我们点进去看 left 和 right 都表示索引，使用无符号右移又不怕整型溢出，那就用 int mid = (left + right) >>> 1 好啦。位运算本来就比使用除法快，这样看来使用 + 和 <<< 真的是又快又好了。

我想这一点可能是 JDK8 的编写者们更层次的考量。

看来以后写算法题，就用 int mid = (left + right) >>> 1 吧，反正更多的时候 left 和 right 表示索引。

8、编码一旦出现死循环，输出必要的变量值、分支逻辑是调试的重要方法。
当出现死循环的时候的调试方法：打印输出左右边界、中位数的值和目标值、分支逻辑等必要的信息。

按照我的经验，一开始编码的时候，稍不注意就很容易出现死循环，不过没有关系，你可以你的代码中写上一些输出语句，就容易理解“在区间元素只有 2 个的时候容易出现死循环”。具体编码调试的细节，可以参考我在「力扣」第 69 题：x 的平方根的题解《二分查找 + 牛顿法（Python 代码、Java 代码）》 。

总结

总结一下，我爱用这个模板的原因、技巧、优点和注意事项：

原因：
无脑地写 while left < right: ，这样你就不用判断，在退出循环的时候你应该返回 left 还是 right，因为返回 left 或者 right 都对；

技巧：
先写分支逻辑，并且先写排除中位数的逻辑分支（因为更多时候排除中位数的逻辑容易想，但是前面我也提到过，这并不绝对），另一个分支的逻辑你就不用想了，写出第 1 个分支的反面代码即可（下面的说明中有介绍），再根据分支的情况选择使用左中位数还是右中位数；

说明：这里再多说一句。如果从代码可读性角度来说，只要是你认为好想的逻辑分支，就把它写在前面，并且加上你的注释，这样方便别人理解，而另一个分支，你就不必考虑它的逻辑了。有的时候另一个分支的逻辑并不太好想，容易把自己绕进去。如果你练习做得多了，会形成条件反射。

我简单总结了一下，左右分支的规律就如下两点：

如果第 1 个分支的逻辑是“左边界排除中位数”（left = mid + 1），那么第 2 个分支的逻辑就一定是“右边界不排除中位数”（right = mid），反过来也成立；

如果第 2 个分支的逻辑是“右边界排除中位数”（right = mid - 1），那么第 2 个分支的逻辑就一定是“左边界不排除中位数”（left = mid），反之也成立。

“反过来也成立”的意思是：如果在你的逻辑中，“边界不能排除中位数”的逻辑好想，你就把它写在第 1 个分支，另一个分支是它的反面，你可以不用管逻辑是什么，按照上面的规律直接给出代码就可以了。能这么做的理论依据就是“排除法”。

在「力扣」第 287 题：寻找重复数的题解《二分法（Python 代码、Java 代码）》和这篇题解的评论区中，有我和用户
@fighterhit 给出的代码，在一些情况下，我们先写了不排除中位数的逻辑分支，更合适的标准就是“哪个逻辑分支好想，就先写哪一个”，欢迎大家参与讨论。

优点：
分支条数只有 2 条，代码执行效率更高，不用在每一轮循环中单独判断中位数是否符合题目要求，写分支的逻辑的目的是尽量排除更多的候选元素，而判断中位数是否符合题目要求我们放在最后进行，这就是第 5 点；

说明：每一轮循环开始都单独判断中位数是否符合要求，这个操作不是很有普适性，因为从统计意义上说，中位数直接就是你想找的数的概率并不大，有的时候还要看看左边，还要看看右边。不妨就把它放在最后来看，把候选区间“夹逼”到只剩 11 个元素的时候，视情况单独再做判断即可。

注意事项 1：
左中位数还是右中位数选择的标准根据分支的逻辑而来，标准是每一次循环都应该让区间收缩，当候选区间只剩下 22 个元素的时候，为了避免死循环发生，选择正确的中位数类型。如果你实在很晕，不防就使用有 22 个元素的测试用例，就能明白其中的原因，另外在代码出现死循环的时候，建议你可以将左边界、右边界、你选择的中位数的值，还有分支逻辑都打印输出一下，出现死循环的原因就一目了然了；

注意事项 2：
如果能确定要找的数就在候选区间里，那么退出循环的时候，区间最后收缩成为 11 个数后，直接把这个数返回即可；如果你要找的数有可能不在候选区间里，区间最后收缩成为 11 个数后，还要单独判断一下这个数是否符合题意。

最后给出两个模板，大家看的时候看注释，不必也无需记忆它们。

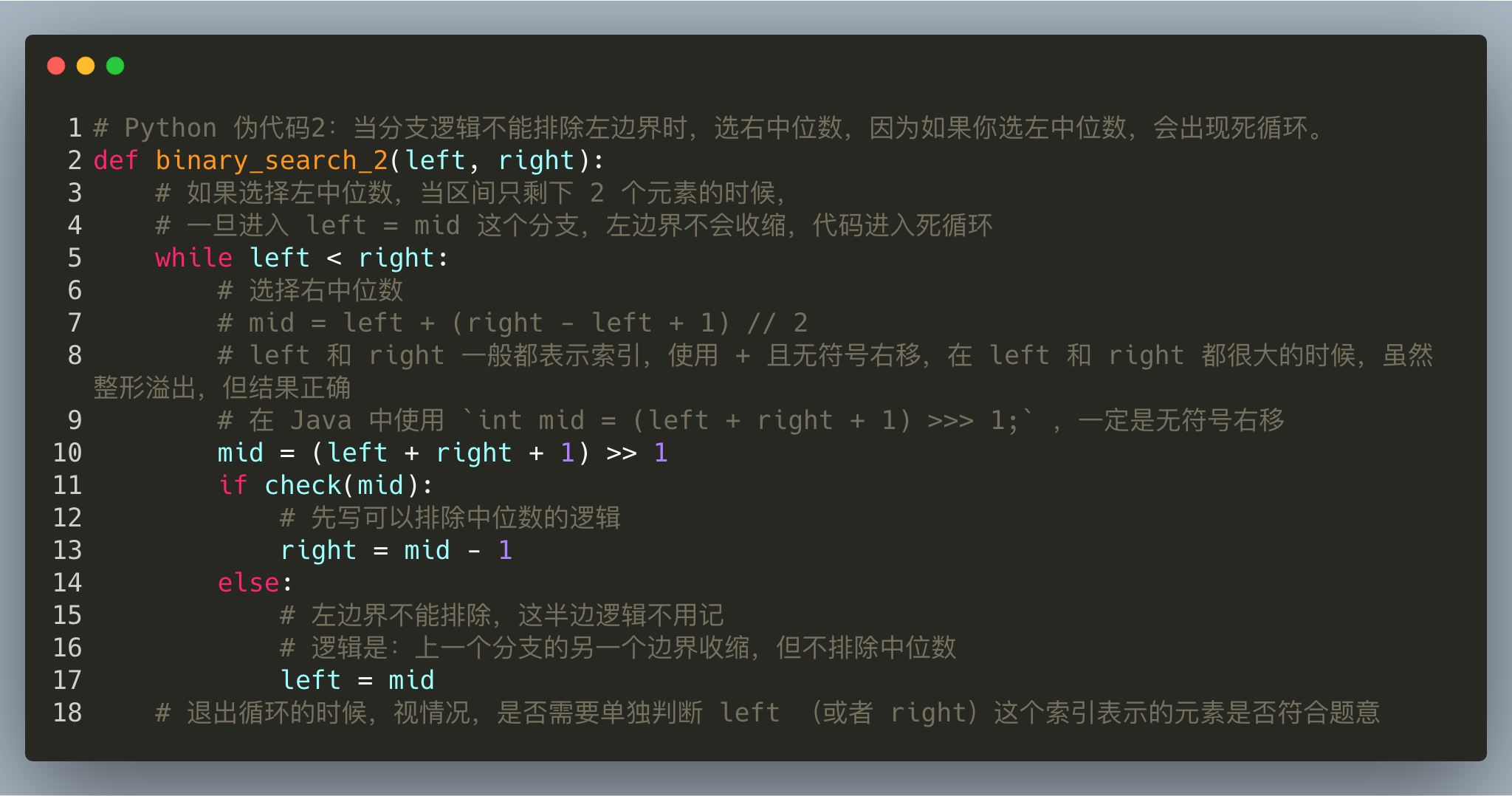
说明：我写的时候，一般是先默认将中位数写成左中位数，再根据分支的情况，看看是否有必要调整成右中位数，即是不是要在 (right - left) 这个括号里面加 11 。

虽说是两个模板，区别在于选中位数，中位数根据分支逻辑来选，原则是区间要收缩，且不出现死循环，退出循环的时候，视情况，有可能需要对最后剩下的数单独做判断。

我想我应该是成功地把你绕晕了，如果您觉得啰嗦的地方，就当我是“重要的事情说了三遍”吧，确实是重点的地方我才会重复说。当然，最好的理解这个模板的方法还是应用它。在此建议您不妨多做几道使用“二分查找法”解决的问题，用一下我说的这个模板，在发现问题的过程中，体会这个模板好用的地方，相信你一定会和我一样爱上这个模板的。

在「力扣」的探索版块中，给出了二分查找法的 3 个模板，我这篇文章着重介绍了第 2 个模板，但是我介绍的角度和这个版块中给出的角度并不一样，第 1 个模板被我“嫌弃”了，第 3 个模板我看过了，里面给出的例题也可以用第 2 个模板来完成，如果大家有什么使用心得，欢迎与我交流。

来源：力扣（LeetCode），作者：liweiwei1419